Options Level 3 Trading
We're excited to support Multi-leg options trading! Use this section to read up on Alpaca's Multi-leg options trading capabilities.
Multi-leg options trading is now available for live trading!
What are Multi-leg Orders?
A multi-leg (MLeg) order is a single, combined order that includes multiple option contracts – calls, puts, or even shares—on the same underlying security. By bundling all legs together, the trade is executed as a single unit and each leg is associated with its own strike price, expiration date, or position type (long or short). MLeg orders are often used when traders need to set up complex strategies with several moving parts. A common example is the call spread, where the trader buys a call option at one strike price while simultaneously selling another call option at a higher strike, both for the same underlying asset.
Why are Multi-leg Orders useful?
MLeg orders are particularly useful because they allow traders to execute complex options or stock combinations in one streamlined process, avoiding the delay or slippage risk of placing each transaction separately. By handling multiple legs at once, traders gain better control over their target price, reduce the chance of partial fills that could distort the intended strategy, and simplify trade management. The potential to minimize transaction costs—whether through tighter spreads, combined commissions, or efficient margin usage, also adds to their appeal.
A trader anticipates a stock will remain in a narrow price range.
They set up an iron condor, which involves four legs:
- Buying one out-of-the-money (OTM) call.
- Selling a call at a closer strike.
- Buying an OTM put.
- Selling another put.
Placing these four legs as a single MLeg order ensures they fill together or not at all.
This reduces the risk of partial fills, which could otherwise leave the trader with unwanted market exposure or unbalanced positions.
How to submit a Multi-leg Order?
To submit a multi-leg (MLeg) order, set your “order_class” to “mleg” and list each component of the strategy in a “legs” array, specifying details like the symbol, side (buy or sell), ratio quantity, and position intent (e.g., buy_to_open). Include any additional parameters (limit price, time in force, etc.) as part of the order’s settings. Below is a cURL example showing how to place a POST request to the Alpaca API, passing in the necessary headers and JSON payload:
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "0.6",
"time_in_force": "day",
"legs": [
{"symbol": "AAPL250117P00200000", "ratio_qty": "1", "side": "buy", "position_intent": "buy_to_open"},
{"symbol": "AAPL250117C00250000", "ratio_qty": "1", "side": "buy", "position_intent": "buy_to_open"}
]
}' | jq -rSome examples
Long Call Spread
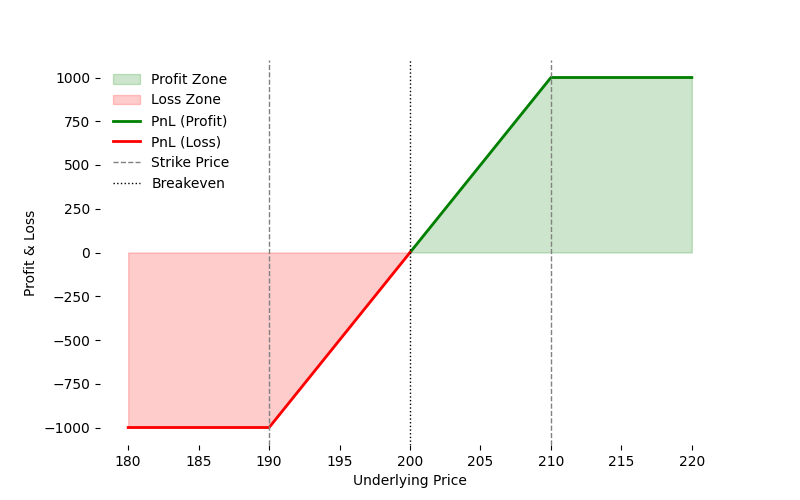
Buy a lower-strike (190) call and sell a higher-strike (210) call on the same underlying:
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "1.00",
"time_in_force": "day",
"legs": [
{
"symbol": "AAPL250117C00190000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
},
{
"symbol": "AAPL250117C00210000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
}
]
}' | jq -rLong Put Spread
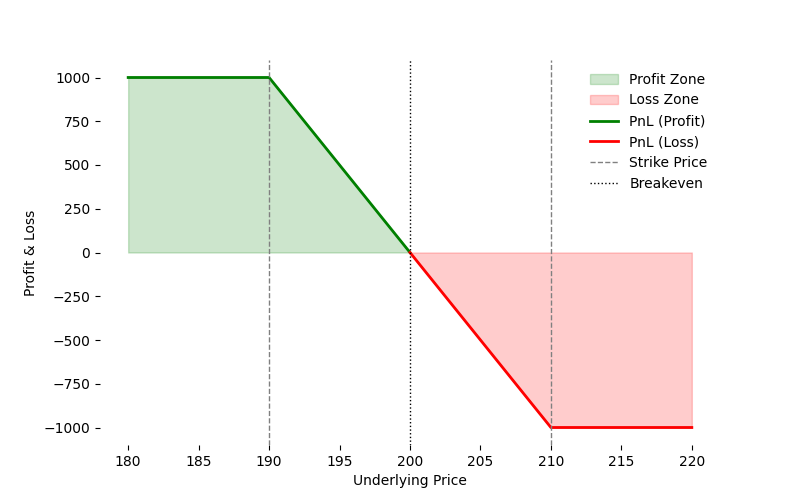
Buy a higher-strike (210) put and sell a lower-strike (190) put on the same underlying:
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "1.25",
"time_in_force": "day",
"legs": [
{
"symbol": "AAPL250117P00210000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
},
{
"symbol": "AAPL250117P00190000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
}
]
}' | jq -rIron Condor
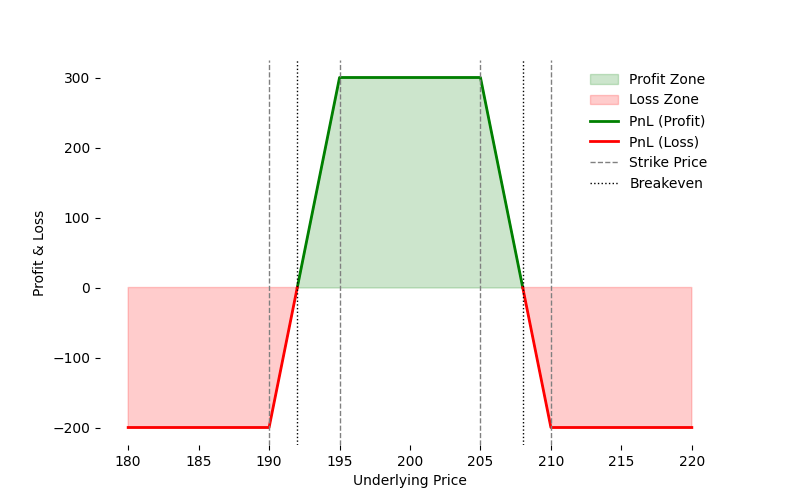
Combine two spreads (a put spread and a call spread) to bet on limited movement:
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "1.80",
"time_in_force": "day",
"legs": [
{
"symbol": "AAPL250117P00190000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
},
{
"symbol": "AAPL250117P00195000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
},
{
"symbol": "AAPL250117C00205000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
},
{
"symbol": "AAPL250117C00210000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
}
]
}' | jq -rLearn about the differences between an iron condor and iron butterfly.
Roll a Call Spread (strike price)
Close an existing short call spread and open a new one at different strikes in a single transaction:
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "2.05",
"time_in_force": "day",
"legs": [
{
"symbol": "AAPL250117C00200000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_close"
},
{
"symbol": "AAPL250117C00205000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_close"
},
{
"symbol": "AAPL250117C00210000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
},
{
"symbol": "AAPL250117C00215000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
}
]
}' | jq -rRoll a Call Spread (expiration date)
Below is an example of rolling a short call spread from one expiration date to another in a single multi-leg (MLeg) order. The first two legs (with symbols ending in 250117) are closed (buy_to_close and sell_to_close), and the new positions are opened at later-dated strikes (250224):
curl --request POST \
--url $APIDOMAIN/v2/orders \
--header 'accept: application/json' \
--header 'content-type: application/json' \
--header "Apca-Api-Key-Id: $APIKEY" \
--header "Apca-Api-Secret-Key: $SECRET" \
--data '
{
"order_class": "mleg",
"qty": "1",
"type": "limit",
"limit_price": "2.05",
"time_in_force": "day",
"legs": [
{
"symbol": "AAPL250117C00200000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_close"
},
{
"symbol": "AAPL250117C00205000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_close"
},
{
"symbol": "AAPL250124C00200000",
"ratio_qty": "1",
"side": "sell",
"position_intent": "sell_to_open"
},
{
"symbol": "AAPL250124C00205000",
"ratio_qty": "1",
"side": "buy",
"position_intent": "buy_to_open"
}
]
}' | jq -rSome deeper explanations
How do we calculate maintenance margin requirements?
-
Ignore Premiums
When calculating maintenance margin, do not factor in the premiums paid or received. Instead, focus on the intrinsic (exercise) payoffs. -
Model Each Option’s Payoff
Each option is represented by a piecewise linear payoff function (PnL) based on the underlying price (p).
-
Combine Positions
To determine total payoff, sum the piecewise functions for all open positions: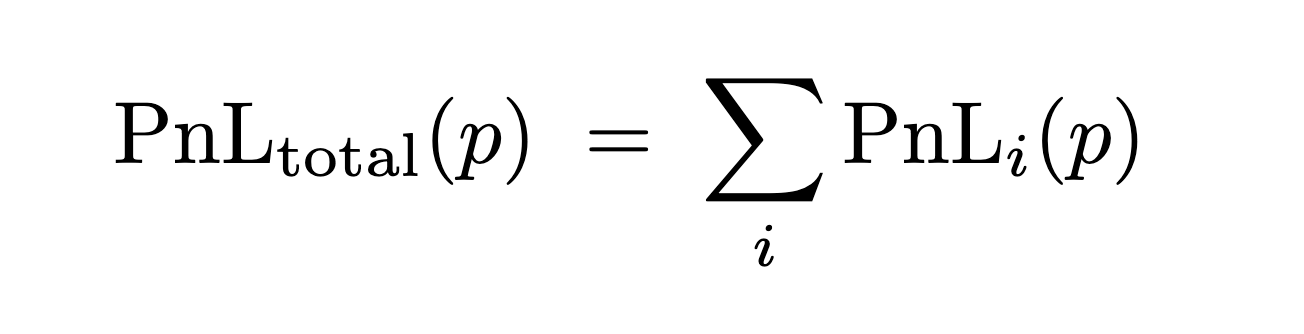
-
Find Theoretical Maximum Loss
Maintenance margin is based on the worst-case scenario for the portfolio: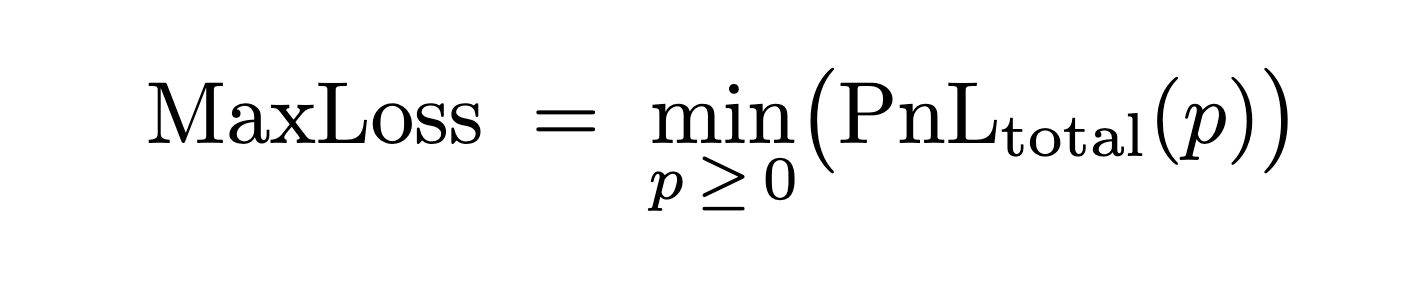
In other words, you determine the underlying price p that yields the lowest (most negative) net payoff. The absolute value of this lowest point is the margin requirement.
- Different Expirations
For option positions with multiple expiration dates, calculate this theoretical maximum-loss approach separately for each expiration date, then use the largest resulting requirement across all expirations.
Lets see an example in order to understand why this way of calculating the maintenance margin is benefiting the customers.
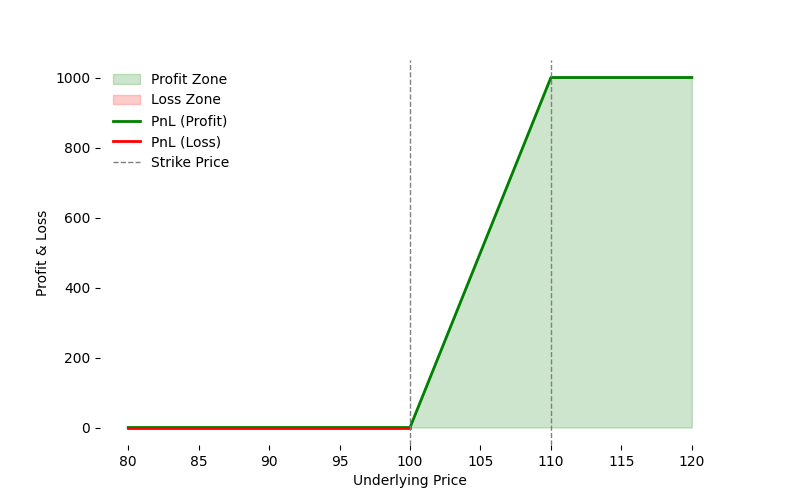
Lets assume that a customer has the following positions
- Long Call for AAPL with Strike Price = 100
- Short Call for AAPL with Strike Price = 110
- Long Call for AAPL with Strike Price = 200
- Short Call for AAPL with Strike Price = 190
Using the traditional way of calculating maintenance margin we would form 2 spreads
Spread 1 (Call Credit Spread):
- Long Call for AAPL with Strike Price = 200
- Short Call for AAPL with Strike Price = 190
With maintenance margin = 1000 since the difference between strike prices is 10 and the option’s multiplier is 100 so the maintenance_margin = strike_price_diff * multiplier
Spread 2 (Call Debit Spread):
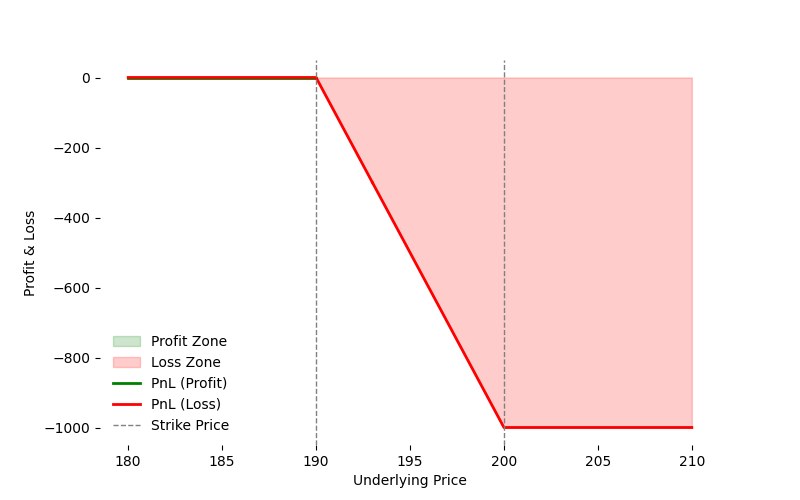
- Long Call for AAPL with Strike Price = 100
- Short Call for AAPL with Strike Price = 110
With maintenance margin = 0 since the difference between strike prices is 10 but the long is higher than the short.
So the Total Maintenance Margin (Traditional) = 1000 + 0 = $1000
Universal Spread Rule Calculation
When combining all four positions and evaluating the theoretical maximum combined loss, the payoff analysis shows that losses from one spread offset gains or losses in the other, resulting in a net theoretical maximum loss of zero. Hence:
- Total Maintenance Margin (Universal Spread) = $0
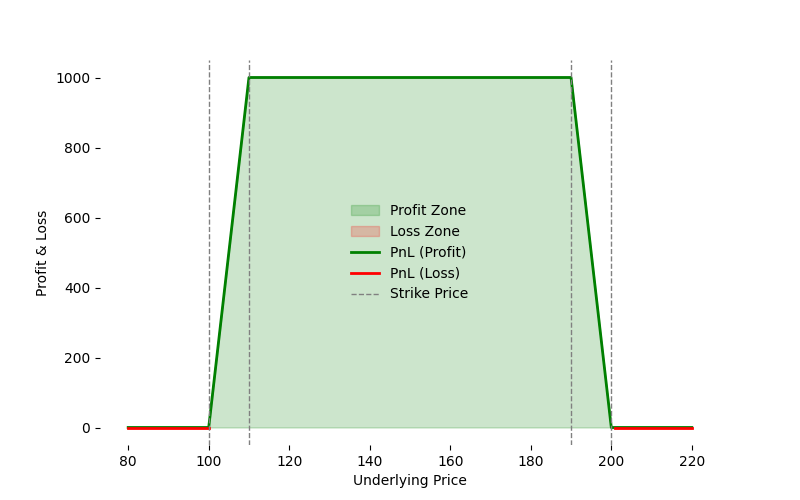
This “universal spread rule” or piecewise-payoff approach better reflects the true risk when these positions are considered together. By recognizing how the different calls offset one another’s exposures, the required margin is lower—benefiting the customer by aligning margin requirements with the actual worst-case scenario of the entire portfolio rather than assigning sums of individual spreads.
References:
https://cdn.cboe.com/resources/membership/Margin_Manual.pdf
First, compute the intrinsic value of the options at price points for the underlying security or instrument that are set to correspond to every exercise price present in the spread. Then, net the intrinsic values at each price point. The maximum potential loss is the greatest loss, if any, from among the results.
https://cdn.cboe.com/resources/regulation/rule_filings/margin_requirements/SR-CBOE-2012-043.pdf
(A) For spreads as defined in subparagraph (a)(5) of this Rule, the long options
must be paid for in full. In addition, margin is required equal to the lesser of the
amount required for the short option(s) by subparagraph (c)(5)(A) or (B),
whichever is applicable, or the spread’s maximum potential loss, if any. To
determine the spread’s maximum potential loss, first compute the intrinsic value
of the options at price points for the underlying security or instrument that are set
to correspond to every exercise price present in the spread. Then, net the intrinsic
values at each price point. The maximum potential loss is the greatest loss, if any,
from among the results. The proceeds for establishing the short options may be
applied toward the cost of the long options and/or any margin requirement.
How do we calculate order cost basis?
Definition:
The cost basis of a multi-leg (MLeg) order is the sum of:
- The maintenance margin required for the combined positions (as determined by the universal spread rule), and
- The net price (debit/credit) from buying or selling the option contracts.
Example:
Consider a call credit spread on AAPL:
- Long Call (buy) for AAPL with Strike Price = 200
- Short Call (sell) for AAPL with Strike Price = 190
Maintenance Margin: Universal spread rule requires a margin of $1,000 for this spread.
Net Option Price:
- The long call premium to be paid is $10 (cost to the buyer).
- The short call premium to be received is $15 (credit to the seller).
- Net Price = (15−10)=(15 - 10) =$5 credit
- Because each option contract covers 100 shares, multiply by 100:
Net Price (per contract) x 100 = 5 x 100 = $500 - However, for cost-basis purposes, a credit (positive $5) effectively reduces the overall cost, so it becomes -$5 in the order’s net debit/credit calculation.
So, Total Cost Basis:
Cost Basis = (Maintenance Margin) + (Net Price×Option Multiplier) = 1000 + (-5 x 100) = 1000 - 500 = $500
Hence, the cost basis—and the amount charged to the customer—for this multi-leg order is $500.
Some Edge Scenarios
GCD ratio_qty requirement
ratio_qty requirementWhen submitting an MLeg order, each leg’s leg_ratio must be in its simplest form. In other words, the greatest common divisor (GCD) among the leg_ratio values for the legs must be 1.
Example (wrong)
- Leg 1:
leg_ratio = 4 - Leg 2:
leg_ratio = 2
Because both ratios share a common divisor of 2, the system will reject this order. If a ratio must be 2:4, for instance, the user should enter it as 1:2 instead (dividing both sides by the GCD of 2).
Reason for Enforcing Simplified Ratios
By requiring that leg ratios be in their simplest form (prime to each other), the system can:
Avoid Redundant Parent Quantities: The ratio is intended to show the relative proportions of each leg; if the ratio isn’t simplified, you’re effectively duplicating the same information already available through the parent order quantity.
This approach ensures clarity in trade definitions and prevents potential confusion or errors in calculating fill quantities and margin requirements.
Restrictions on Combo Order(equity leg + contract leg)
MLeg orders that include an equity leg are not supported at this time. This means that combining an equity position with an options contract in a single order is not currently available for any trading strategy.
MLeg restrictions regarding uncovered legs
Starting on day zero of Options Level 3 trading, an MLeg order is accepted only if all its legs are covered within the same MLeg order. For example, an MLeg order containing two short call legs would be rejected, though submitting those short calls separately as single-leg orders is allowed. This restriction also impacts certain strategies, including rolling a short contract or rolling a calendar spread, since they would involve uncovered short legs within the same multi-leg order.
The content of this article is for general informational purposes only. All examples are for illustrative purposes only.
Options trading is not suitable for all investors due to its inherent high risk, which can potentially result in significant losses. Please readCharacteristics and Risks of Standardized Options before investing in options.
All investments involve risk, and the past performance of a security, or financial product does not guarantee future results or returns. There is no guarantee that any investment strategy will achieve its objectives. Please note that diversification does not ensure a profit, or protect against loss. There is always the potential of losing money when you invest in securities, or other financial products. Investors should consider their investment objectives and risks carefully before investing.
Securities brokerage services are provided by Alpaca Securities LLC ("Alpaca Securities"), memberFINRA/SIPC, a wholly-owned subsidiary of AlpacaDB, Inc. Technology and services are offered by AlpacaDB, Inc.
This is not an offer, solicitation of an offer, or advice to buy or sell securities or open a brokerage account in any jurisdiction where Alpaca Securities are not registered or licensed, as applicable.
Updated 6 months ago